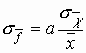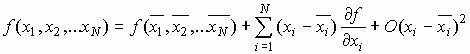
Σε πειράματα στα οποία το επιθυμητό αποτέλεσμα προσδιορίζεται από δύο ή περισσότερες ποσότητες (πχ η αντίσταση υπολογίζεται από το λόγο της τάσης προς το ρεύμα), τα σφάλματα κάθε ποσότητας συνδυάζονται για να δώσουν την αβεβαιότητα στο τελικό αποτέλεσμα.
Στη γενική περίπτωση, ας θεωρήσουμε τη συνάρτηση
f(x1, x2,…xN), η οποία εξαρτάται από τις τυχαίες μεταβλητές x1, x2,…xN. Οι τιμές των x1, x2,…xN προσδιορίζονται πειραματικά και στη συνέχεια υπολογίζεται η τιμή της συνάρτησης f(x1, x2,…xN). Εφόσον οι τιμές των παραμέτρων xi προσδιορίστηκαν πειραματικά, θα έχουν επίσης εκτιμηθεί οι τιμές των μέσων1.
Ποια είναι η αντιπροσωπευτική τιμή της συνάρτησης f;2.
Ποιο είναι το τυπικό σφάλμα στον υπολογισμό της f; Θεωρούμε ότι η συνάρτηση f(x1, x2,…xN) μπορεί να αναλυθεί σε σειρά Taylor στην περιοχή των μέσων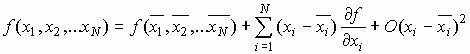
όπου με
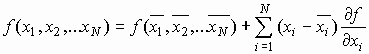
Για την απάντηση του πρώτου ερωτήματος θεωρούμε ότι η αντιπροσωπευτική τιμή της συνάρτησης f(x1, x2,…xN) είναι η μέση τιμή:
![]()
Η τυπική απόκλιση της συνάρτησης f(x1, x2,…xN) βρίσκεται:
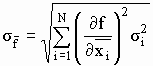
η οποία χρησιμοποιείται για τον υπολογισμό του σφάλματος μιας σύνθετης μέτρησης.
Στη συνέχεια θα υπολογίσουμε την τυπική απόκλιση συναρτήσεων που χρησιμοποιούνται συχνά στην πειραματική ανάλυση. Οι συναρτήσεις αυτές είναι συναρτήσεις μιας ή περισσοτέρων μεταβλητών xi και σταθερών αi.1)
Άθροισμα:![]() ,
,
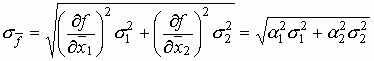
2) Γενική περίπτωση αθροίσματος:
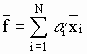 .
.
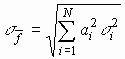
Παρατηρούμε ότι στην πρόσθεση (και στην αφαίρεση), η απόλυτη αβεβαιότητα στο αποτέλεσμα είναι συνδυασμός των τετραγώνων των απολύτων αβεβαιοτήτων των αρχικών μεταβλητών.
3)
Γινόμενο:![]()
![]()
Είναι εύκολο να αποδειχτεί ο απλούστερος τύπος:
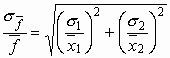
4)
Πηλίκο: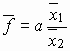
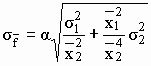
Όπως και στη περίπτωση του γινομένου είναι εύκολο να δειχτεί:
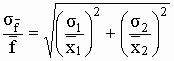
Παρατηρούμε ότι η προηγούμενη σχέση εκφράζει το σχετικό σφάλμα του γινομένου ή του πηλίκου, το οποίο είναι ίσο με την τετραγωνική ρίζα του αθροίσματος των τετραγώνων των σχετικών σφαλμάτων των μεταβλητών x1 και x2.
5) Δύναμη:
![]() , όπου
ν είναι πραγματικός αριθμός.
, όπου
ν είναι πραγματικός αριθμός.
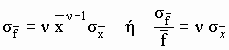
6)
Εκθετική συνάρτηση:![]()
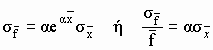
7) Λογάριθμος
![]()